DESIGN FOR ADDITIVE MANUFACTURING: SIMULACIÓN POR MÉTODOS DE ELEMENTOS FINITOS
Las posibilidades que ofrece la fabricación aditiva en términos de diseño permite la creación de soluciones con geometrías sin precedentes en el ámbito industrial. Con esta tecnología se pueden, además de crear geometrías muy complejas difícilmente alcanzables mediante otras técnicas, introducir estructuras internas que aligeren las piezas o añadir localmente formas que mejoren alguna propiedad.
Estas geometrías complejas complejas frecuentemente tienen similitudes con formas orgánicas que maximizan las propiedades minimizando el consumo de material (al igual que las formas en la naturaleza) y resultan atractivas a la vez que funcionales; estás formas se definen con criterios basados en la funcionalidad de cada pieza y con el objetivo de obtener soluciones optimas minimizando el uso de material pero cumpliendo con los requisitos de trabajo de la pieza.
Toda esta complejidad geométrica implica a su vez una dificultad añadida a la hora de entender y prever los comportamientos estructurales, haciendo no tan evidente el diseño, y es por ello que herramientas complementarias al CAD como la optimización topológica o la simulación por métodos de elementos finitos adquieren un papel clave en el proceso de Design For Addtive Manufacturing (DFAM).
La simulación por el método de los elementos finitos es un recurso muy extendido en el ámbito de la ingeniería y consiste en el análisis numérico de un determinado sistema físico (análisis estructural, dinámica de fluidos, transferencia de calor…), donde es necesario definir un dominio o espacio de interés y unas condiciones de contorno.
La simulación por métodos de elementos finitos es un recurso muy extendido en el ámbito de la ingeniería y consiste en el análisis numérico de un determinado sistema físico.
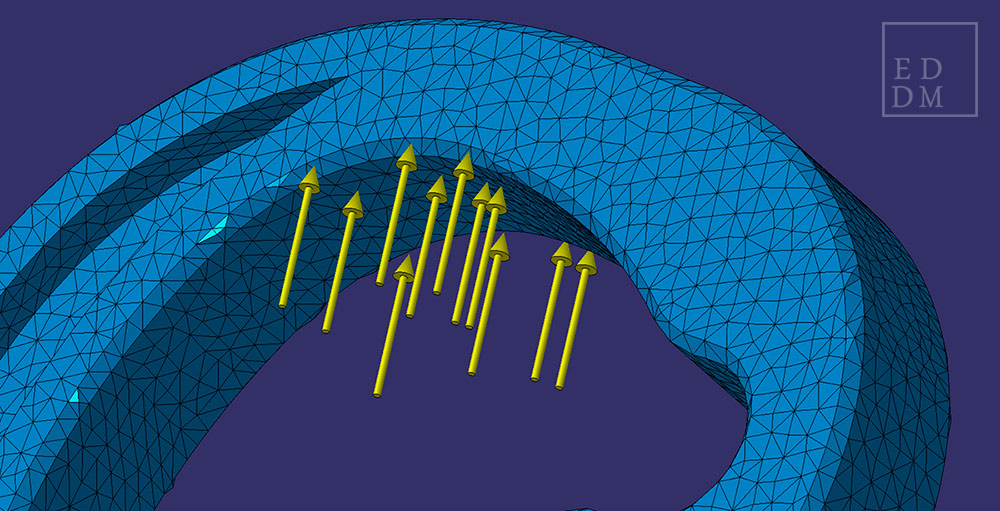
En el caso de cálculo estructural de una pieza el dominio se refiere a la geometría en cuestión, que se fracciona en múltiples elementos (simples, como triángulos o cuadrados) interconectados y donde las ecuaciones que rigen sus respectivos comportamientos son equivalentes a las de la pieza entera en lo que se conoce como discretización. Las condiciones de contorno hacen referencia a elementos externos a la pieza en sí como pueden ser las cargas aplicadas, interfaces con el entorno como las uniones, condiciones térmicas, condiciones de vibraciones, etc. Asimismo, es necesario asignar un material y con él sus propiedades físicas y mecánicas.
Este conjunto de operaciones se conoce como modelización. Todo este proceso se conoce como pre proceso.
Le sigue la simulación en sí misma, que consiste en la operación computacional que resuelve las ecuaciones de cada uno de los nodos de los elementos y proporciona información relativa al caso planteado, como tensiones soportadas o deformaciones producidas. La resolución del problema en sí la realiza un código que se conoce como solver.
La última fase del proceso del cálculo por elementos finitos es el tratamiento de los resultados proporcionados por el solver que generalmente realiza el mismo programa y se denomina post proceso.
Generalmente, la modelización de un sistema complejo requiere trabajo y experiencia, y su simulación puede tardar horas o incluso días dependiendo de la potencia computacional a disposición y del nivel de complejidad del sistema. También se utiliza en casos donde la experimentación empírica es difícil, costosa o peligrosa.
Sin embargo, integrado en el proceso de DFAM la aplicación de esta herramienta es más superficial, entendido como un uso que no explota todo el potencial de la simulación por métodos de elementos finitos.
Principalmente por la característica de anisotropía que acusan las piezas producidas a través de FA en general y FDM en particular, los resultados obtenidos de una simulación por métodos de elementos finitos no tienen la fiabilidad que pueda tener la simulación de una pieza inyectada (isótropa).
La última fase del proceso del cálculo por elementos finitos es el tratamiento de los resultados proporcionados por el solver que generalmente realiza el mismo programa y se denomina post proceso.
[twenty20 img1=»27693″ img2=»27692″ direction=»horizontal» offset=»0.5″ align=»left» width=»50%» before=»Antes» after=»Después» hover=»true»]
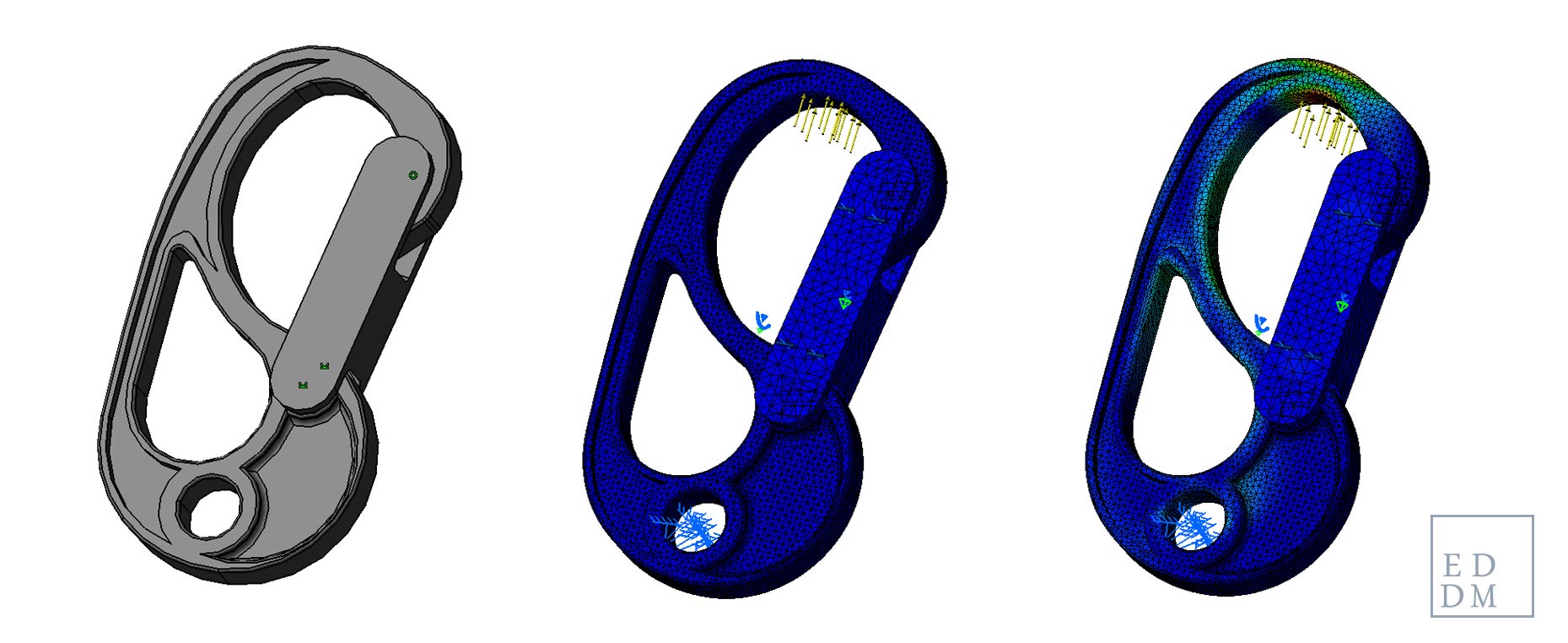
|Deformación y mapa de presiones tras la aplicación de caso de carga. Fuente EDDM.
No servirá como método de validación, por ejemplo, pero si será muy útil a la hora de orientar las decisiones de diseño. Deja de ser un medio para la consecución de un hito (validación), pero de la misma manera el trabajo riguroso requerido en una modelización precisa desaparece, e igualmente sucede con el tiempo de computación.
Durante el proceso de diseño de una pieza compleja, la intuición o las analogías son más difíciles de aplicar, como se ha dicho antes, y la simulación por métodos de elementos finitos con un planteamiento simplificado se convierte en una operación rápida pero concluyente. Combinada con la prototipado rápido y utilizada en forma de “loop”, puede suponer un elemento diferencial en el proceso de diseño.
Por tanto, es necesario entender cómo las características de la fabricación aditiva, en este caso la transición de fundido/sólido durante la consolidación del cuerpo, afecta a las propiedades mecánicas de la pieza (induce anisotropía) y también al modo y los objetivos con los que se utilizan las herramientas ingenieriles. Y una vez más, el criterio de la persona es el que marca la diferencia.